গাণিতিক গড়(Average) নির্ণয়, সহজ পদ্ধতিতে গড় নির্ণয় ও গড়(Average) মানে কি?

 (BCS প্রিলিমিনারিতে সেট, বিন্যাস,গড়(Average) ও সমাবেশ, পরিসংখ্যান ও সম্ভাব্যতা থেকে সর্বোচ্চ ০৩ নম্বর থাকবে এবং অন্যান্য প্রতিযোগিতামূলক পরীক্ষায়ও এ অধ্যায়গুলো থেকে প্রশ্ন থাকে)

বীজগনিত বা পাটিগণিতে পরিসংখ্যান বা Statistics অধ্যায়ে বা তথ্য উপাত্য অধ্যায়ে গড়(Average) বা গাণিতিক গড়(Average) কি, কাকে বলে বা গড়(Average) করার নিয়ম সম্পর্কে ভয় ও বিভ্রান্তি লক্ষ্য করা যায়। কিভাবে সমাধান করবো, গড় (Average) ও গাণিতিক গড় নির্ণয়ের পদ্ধতি কি একই? সংক্ষিপ্ত ও সহজ পদ্ধতিতে কিভাবে গড় নির্ণয় করতে হয়? এমন নানান প্রশ্ন দেখা দেয় ছাত্র ছাত্রীদের মনে।

৫ম, ৬ষ্ঠ, ৭ম, ৮ম, ৯ম, ১০ম থেকে শুরু করে এইচএসসি বা ১১-১২ শ্রেণি এমনকি অনার্স মাস্টার্স লেভেলেও গড় বিষয়টি খুবি গুরুত্বপূর্ণ। আজকের আলোচনা গড় সম্পর্কে বিস্তারিত। সহজ, সংক্ষিপ্ত ও কৌশলগত মজার পদ্ধতি প্রয়োগ করে বিষয়টি এমন ভাবে উপস্থাপন করা হয়েছে, আশাকরি সকলে গড় সম্পর্কে না বুঝে আর থাকবো না।

 গড়(Average) মানে কি?

সাধারণভাবে গড় (Average) হলো এক রাশি সংখ্যার প্রতিনিধিস্থানীয় একটি মান। যেমন একটি বাসায় যদি পাঁচ জন মানুষ থাকে এবং তাদের বয়স যদি ১২, ১৬, ১৮, ৩৪ এবং ৩৮ হয় তবে তাদের “গড় বয়স” কত সে প্রশ্নটি প্রাসঙ্গিক। এখানে ১২, ১৬, ১৮, ৩৪, ৩৮ একটি রাশি, প্রতিটি সংখ্যা একটি উপাত্ত এবং “গড় বয়স” একটি পরিসংখ্যান।

গণিতে কোনো উপাত্তের “গড়” বা “কেন্দ্রপ্রবণতা” বলতে সেই উপাত্তের “প্রতিনিধিস্থানীয়” বা “মাঝামাঝি মান” বোঝায়। পরিসংখ্যানে গড় বা কেন্দ্রীয় প্রবণতা পরিমাপের বিভিন্ন পদ্ধতি রয়েছে যেমন, গাণিতিক গড়, মধ্যক এবং প্রচুরক। অন্যান্য পরিসংখ্যানিক পরিমাপ যেমন স্টান্ডার্ড ডেভিয়েশন (পরিমিত গণক) এবং রেঞ্জ (বিস্তার) এদেরকে ব্যাপ্তির পরিমাপ বলা হয়। এদের দ্বারা উপাত্তের ব্যপ্তি বা এর মানসমূহ কতটুকু ছড়িয়ে আছে বোঝা যায়।

গড়(Average) হচ্ছে কোনো একটা সংখ্যা তালিকা বা রাশির সকল মানকে প্রতিনিধিত্বকারী একটি একক মান। কোনো তালিকার সব সংখ্যার মান যদি সমান হয় তাহলে সেই সংখ্যাটিই সেই তালিকার প্রতিনিধিত্বকারী মান। যদি সমান না হয়, তাহলে প্রতিনিধিত্বকারী মান হিসেবে সেই তালিকা থেকে দৈবচয়ন পদ্ধতিতে কোনো একটা সংখ্যাকে বাছাই করা যেতে পারে।

যদিও ‘গড়’ বলতে নির্দিষ্ট ভাবে দৈবচয়নের চেয়ে ভালো কোনো গাণিতিক উপায়ে বাছাই করা এবং ব্যবহারীক ক্ষেত্রে কার্যকর সংখ্যাকেই বোঝায়। সে ক্ষেত্রে, তালিকার সব সংখ্যাকে নির্দিষ্ট কোনো গাণিতিক উপায়ে মিলিয়ে একটি গড় মান নির্ণয় করা হয়।

গড়(Average) নির্ণয়ের সবচেয়ে প্রচলিত পদ্ধতি হচ্ছে গাণিতিক গড়। এ ছাড়াও কেন্দ্রপ্রবণতা পরিমাপের আরও অনেক পদ্ধতি আছে। যেমন, একটি হচ্ছে মধ্যক বা মেডিয়ান। ঘর-বাড়ির দাম বা মানুষের আয়ের উপাত্তে গাণিতিক গড়ের বদলে মধ্যক ব্যবহৃত হয়। কারণ এধরনের উপাত্তে মানগুলোর বিস্তার সুষম থাকে না, বা কোনো একদিকে অল্প কিছু বৃহৎ মানের সংখ্যা থাকে।

গড় (Average) হলো এক রাশি সংখ্যার প্রতিনিধিস্থানীয় একটি মান। ১২, ১৬, ১৮, ৩৪, ৩৮ একটি রাশি, প্রতিটি সংখ্যা একটি উপাত্ত এবং “গড়(Average) বয়স” একটি পরিসংখ্যান। গণিতে কোনো উপাত্তের “গড়(Average)” বা “কেন্দ্রপ্রবণতা” বলতে সেই উপাত্তের “প্রতিনিধিস্থানীয়” বা “মাঝামাঝি মান” বোঝায়।

গড়ের(Average) প্রকারভেদঃ

গড়কে(Average) নানান ভাবে প্রকরণ করা যেতে পারে। বিশ্লেষণ ও ক্ষেত্রগত দিক দিয়ে গড় কে ৩ টি ভাগে ভাগ করা হয়ে থাকে। অর্থাৎ গড় ৩ প্রকার। যথা-

• ১. গাণিতিক গড়(Average) বা Arithmetic Mean (এটি মূলত পাঠ্য বইয়ে থাকা গড়, যা নিয়ে এখানে বিস্তারিত আলোচনা হবে) 
• ২. গুণিতক গড়(Average) বা Geometric Mean (আনুপাতিক হিসাব, পরিবর্তন বা শতকরা হিসাবের গড় বের করতে ব্যাবসা প্রতিষ্ঠানে এই পদ্ধতিতে গড় বের করা হয়, নিম্ন শ্রেণীর পাঠ্য বইয়ে এ পদ্ধতি না থাকায় এ বিষয়ে এখানে আলোচনা করা হবে না) 
• ৩. তরঙ্গ গড়(Average) বা Harmonic Mean (শেয়ার প্রতি গড় আয়, টাকা প্রতি গড় আয় বা এমন ক্ষেত্রে এই পদ্ধতিতে গড় নির্ণয় করা হয়ে থাকে, নিম্ন শ্রেণীর পাঠ্য বইয়ে এ পদ্ধতি না থাকায় এখানে আলোচনা করা হবে না)

গাণিতিক গড়(Average) কি বা কাকে বলেঃ

গড়(Average) বলতে গাণিতিক গড়কেই বোঝায়। ৫ম, ৬ষ্ঠ, ৭ম, ৮ম, ৯ম, ১০ম বা উচ্চ শ্রেণীতে আমরা পরিসংখ্যান বা তথ্য উপাত্ত অধ্যায়ে যে গড় করি তা মূলত গাণিতিক গড়। গণিতের সূত্র প্রয়োগ করে গড় নির্ণয় করাকে গাণিতিক গড় বলে। অর্থাৎ এটা স্পষ্ট যে আমরা নিজ নিজ শ্রেণীতে যতো প্রকার গড় নির্ণয় করি তার সকল পদ্ধতি কেই গাণিতিক গড় বলে। তাই পরীক্ষায় গাণিতিক গড় করতে বললে বিশেষ কোনো পদ্ধতিতে গড় করতে হবে না। তুমি যতো প্রকারের গড় করেছো বা যে যে সূত্র ব্যবহার করে যে যে পদ্ধতিতে গড় নির্ণয় করেছো তার সবি গাণিতিক গড় বা গড়। ইংরেজীতে গড় বা গাণিতিক গড়কে Arithmetic mean বলা হয়ে থাকে।

এক নজরে গড়(Average) নির্ণয়ের পদ্ধতি সমূহঃ

নিচের চিত্রে ছক বা চার্ট আকারে গড়(Average) নির্ণয়ের পদ্ধতি সমূহ তুলেধরা হলো। আশাকরি চার্ট বা ছকটি গাণিতিক গড় বা গড় নির্নয়ের জন্য খুবি সহায়ক হবে-

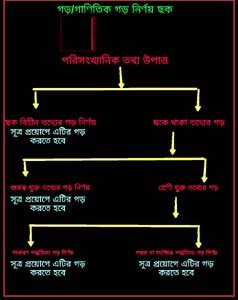
গড়(Average) নির্ণয়ের সূত্রঃ

গড়(Average) বলতে আমরা গাণিতিক গড়কে বুঝি। তাই বই এর সকল সূত্র বা পদ্ধতিই গাণিতিক গড় বা গড়। অপর দিকে তথ্য উপাত্ত বই এ ২ ভাবে দেওয়া থাকে, যথা-

• ১. ছক বিহীন তথ্য 
• ২. ছকে থাকা তথ্য

নিম্নে ছক বিহীন থাকা তথ্যের গড়(Average) বা গাণিতিক গড় নির্ণয়ের সূত্র বা পদ্ধতি সহজ ভাবে তুলে ধরা হলো।

ছক বিহীন তথ্যের গড়(Average) নির্ণয়ের সূত্রঃ

ছক বিহীন তথ্যের গড়(Average) বা গাণিতিক গড় নির্ণয়ের সূত্রটি হলো-

গড় (Average)বা গাণিতিক গড় = রাশি সমষ্টি ÷ রাশি সংখ্যা।

এখানে রাশিগুলোর সমষ্টি বলতে তথ্য উপাত্তের সমষ্টিকে বোঝানো হয়েছে এবং রাশি সংখ্যা বলতে তথ্য উপাত্তে থাকা গণসংখ্যাকে বোঝানো হয়েছে।

উদাহরণঃ

৩০, ১৫, ১০, ৩৫, ১০ তথ্য বা ছক বিহীন তথ্য গুলোর গড় বা গাণিতিক গড়(Average) নির্ণয় কর।

সমাধানঃ

প্রদত্ত তত্যের, রাশি সমষ্টি = ৩০ + ১৫ + ১০ + ৩৫ + ১০ = ১০০ এবং রাশি সংখ্যা = ৫ টি অতএব,

গড়(Average) বা গাণিতিক গড়=১০০÷৫=২০

ছকে থাকা তথ্যের গড়(Average) নির্ণয়ের সূত্রঃ

ছকে থাকা তথ্য সাধারন্ত দুটি ভাবে থাকে। যথা-

• ১. গুরুত্ব যুক্ত ছকে থাকা তথ্যের গড়(Average) নির্ণয় 
• ২. শ্রেণী যুক্ত ছকে থাকা তথ্যের গড়(Average) নির্ণয়

গুরুত্ব যুক্ত ছকে থাকা তথ্যের গড়(Average) নির্ণয়ঃ

গুরুত্ব যুক্ত ছকে থাকা তথ্যের গড়(Average) বা গাণিতিক গড় নির্ণয় করতে গেলে গুরুত্ব যুক্ত তথ্য সম্পর্কে আমাদের ধারনার্জন প্রয়োজন। তথ্য গুলো শ্রেণী ব্যাপ্তিতে বিভক্ত না করে যদি ছকে উপস্থাপন করা হয় তখন তাকে গুরুত্ব যুক্ত তথ্য ছক বা সারণী বলে। গণসংখ্যা সারণী থেকে গুরুত্ব যুক্ত তথ্যের গড় বা গাণিতিক গড় নির্ণয়ের জন্য অতিরিক্ত একটি ঘর কাটতে হয়। ঘরটির নাম, তথ্য x গণসংখ্যা। গুরুত্ব যুক্ত তথ্যের গড় বা গাণিতিক গড় নির্ণয়ের সূত্র হলো-

গড়(Average) বা গাণিতিক গড় = (তথ্য x গনসংখ্যর সমষ্টি) ÷ গনসংখ্যা।

নিচে ছবিতে সূত্রটি সুন্দর ভাবে তুলে ধরা হলো

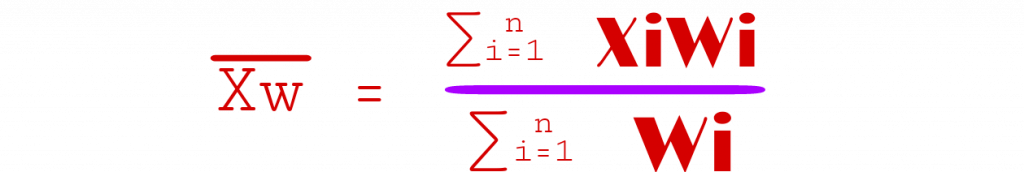
শ্রেণী যুক্ত ছকে থাকা তথ্যের গড়(Average) নির্ণয়ঃ

শ্রেণী যুক্ত বলতে শ্রেণী ব্যাপ্তি আছে এমন তথ্য উপাত্তকে বোঝানো হয়েছে। ৫-১০ বা ১৯-২০ এমন ভাবে শ্রেণীতে তথ্য থাকলে তাকে শ্রেণী যুক্ত তথ্য বলে। শ্রেণী যুক্ত তথ্যের গড়(Average) নির্ণয়ের ২ টি পদ্ধতি রয়েছে। যথা-

• ১. সাধারণ পদ্ধতিতে গড়(Average) নির্ণয় (শ্রেণী যুক্ত ছকে থাকা তথ্য) 
• ২. সংক্ষিপ্ত বা সহজ পদ্ধতিতে গড়(Average) নির্ণয় (শ্রেণী যুক্ত ছকে থাকা তথ্য)

সাধারণ পদ্ধতিতে গড়(Average) নির্ণয়ের সূত্র – ছকে থাকা শ্রেণী যুক্ত তথ্যঃ

ছকে থাকা শ্রেণী যুক্ত তথ্যের গড়(Average) নির্ণয়ের সূত্র হলো-

গড়(Average) বা গাণিতিক গড় = (গণসংখ্যা x মধ্যমানের সমষ্টি) ÷ গণসংখ্যা

অন্যভাবে বলা যায়, গড়(Average) বা গাণিতিক গড়কে x̄, গণসংখ্যাকে fi, গণসংখ্যার সমষ্টিকে n, মধ্যমানকে xi ধরলে, গণসংখ্যা গুণ মধ্যমান হবে fi.xi এবং গণসংখ্যা গুণ মধ্যমানের সমষ্টি হবে ∑fi.xi সুতারং গড় নির্ণয়ের সূত্রটি হবে,

গড়(Average) বা গাণিতিক গড়, x̄=(∑fi.xi)÷n

নিচে ছবিতে সূত্রটি সুন্দর ভাবে তুলে ধরা হলো

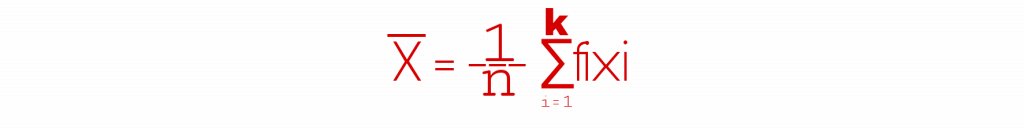
সংক্ষিপ্ত বা সহজ পদ্ধতিতে গড়(Average) নির্ণয়ের সূত্র – ছকে থাকা শ্রেণী যুক্ত তথ্যঃ

সংক্ষিপ্ত বা সহজ পদ্ধতিতে গড়(Average) বা গাণিতিক গড় নির্ণয় করতে গেলে ছকে অতিরিক্ত ৩ টি ঘর বেশি কাটতে হয়। ঘর গুলো হলো-

• ১. মধ্যমান বা xi 
• ২. ধাপ বিচ্যুতি বা ui 
• ৩. গণসংখ্যা x ধাপ বিচ্যুতি বা fi.ui

গড়(Average) বা গাণিতিক গড়কে x̄, গণসংখ্যাকে fi, শ্রেণী ব্যাপ্তি কে h, গণসংখ্যার সমষ্টিকে n, মধ্যমানকে xi, অনুমিত শ্রেণীর মধ্যমানকে a, ধাপ বিচ্যুতি কে ui ধরলে গণসংখ্যা গুণ ধাপ বিচ্যুতি হবে fi.ui এবং গণসংখ্যা গুণ ধাপ বিচ্যুতির সমষ্টি হবে ∑fi.ui সুতারং সংক্ষিপ্ত বা সহজ পদ্ধতিতে গড় নির্ণয়ের সূত্রটি হবে-

গড়(Average) বা গাণিতিক গড় = অনুমিত শ্রেণীর মধ্যমান + (গণসংখ্যা গুণ ধাপ বিচ্যুতির সমষ্টি ÷ গণসংখ্যা) x শ্রেণী ব্যাপ্তি।

অর্থাৎ-

x̄=a+(∑fi.ui÷n).h

নিচে ছবিতে সূত্রটি সুন্দর ভাবে তুলে ধরা হলো-

এখানে, ধাপ বিচ্যুতি নির্ণয়ের জন্যে ছকের মাঝামাঝি একটি ঘরে শূন্য বা ০ ধরতে হয়। ঘর সংখ্যা জোড় হলে মাঝে দুটি ঘর থাকে সে ক্ষেত্রে যে দুটি ঘর মাঝে পড়ে তার নিচের টি তে ০ ধরতে হয়। এই শূন্য ধরা শ্রেণী বা লাইন টি হলো অনুমিত শ্রেণী। যে ঘরে ০ ধরা হবে তার আগের ঘরে -১, তার আগের ঘরে -২, তার আগের ঘরে -৩ এভাবে ঘর গুলো পূর্ণ করতে হবে। আবার যে ঘরে ০ ধরা হবে তার নিচের ঘরে +১, তার নিচের ঘরে +২, তার নিচের ঘরে +৩, তার নিচের ঘরে +৪ এভাবে পূর্ণ করতে হবে। এভাবে ধাপ বিচ্যুতি ঘর বা ui ঘর পূর্ণ করার পর যে ঘরে ০ ধরা হয়েছে সেই লাইনে বাম দিকে মধ্যমানের ঘরে যে মান থাকবে সেই মান হবে অনুমিত শ্রেণীর মধ্যমান বা a এর মান।

গাণিতিক গড়(Average)

n টি সংখ্যার গাণিতিক গড়(Average) বলতে সংখ্যাগুলোর যোগফল কে n দিয়ে ভাগ করে প্রাপ্ত ভাগফল কে বোঝায়। যদি প্রতিটি সংখ্যাকে a_i দিয়ে প্রকাশ করা হয় যেখানে i = 1, …, n তাহলে এদের গাণিতিক গড়(Average) হবে এদের যোগফল ভাগ n বা,{\displaystyle AM={\frac {1}{n}}\sum _{i=1}^{n}a_{i}.}

যেমন দুইটি সংখ্যা 8 ও 2 এর গাণিতিক গড়(Average) A হচ্ছে এমন একটি সংখ্যা যেন, 8+2=A+A। এখান থেকে দেখা যায় A = (8+2)/2 = 5। 2 ও 8 এর ক্রম পরিবর্তন করলেও A এর এই মানের কোনো পরিবর্তন হয় না। গড় মান 5 ক্ষুদ্রতম সংখ্যা 2 এর চেয়ে ছোটোও না আবার বৃহত্তম সংখ্যা 8 এর চেয়ে বড়ও না। আমরা যদি দুই এর অধিক সংখ্যা নিয়েও গড় বের করি যেমন ২,৮ ও ১১ এর জন্যেও ২+৮+১১=A+A+A সমীকরণ থেকে পাবো A = (2+8+11)/3 = 7।

সংখ্যাত্রয়ের ক্রম পরিবর্তন করেও এই গড়(Average) মানের কোনো পরিবর্তন হয় না। অর্থাৎ = (2+11+8)/3 = 7 ই থাকে। যেখানে ৭ এই তালিকার ক্ষুদ্রতম সংখ্যা ২ ও বৃহত্তম সংখ্যা ১১ এর মধ্যবর্তী একটি সংখ্যা। এই যোগফল পদ্ধতিকে সহজেই যেকোনো সংখ্যক উপাদান বিশিষ্ট সংখ্যাতালিকার গড় নির্ণয়ে সাধারণীকরণ করা যেতে পারে।

এখানে উল্লেখ্য যে কয়েকটি পূর্ণ সংখ্যার গড় একটি পূর্ণসংখ্যা নাও হতে পারে। তাই “গড়ে প্রতিটি পরিবারে 1.7 টি সন্তান রয়েছে” শুনলে অবাক হবার কিছু নেই। অবশ্য এভাবে না বলে, “পরিবার সমূহের তালিকা থেকে দেখা যায় তাদের গড় সন্তান সংখ্যা 1.7” এভাবে বললে তথ্যটি আরও ভালো ভাবে প্রকাশ করা( উপাত্তটি প্রকৃষ্ট রূপে উপস্থাপিত) হয়।

গড়(Average) নির্ণয় অংক খুব সহজ।  

মনে করুন দশটি সংখ্যা দেওয়া আছে।  এদের গড়(Average) = সংখ্যা গুলোর সমষ্টি / ১০ 
দশ জন মানুষের বয়সের গড়(Average) = দশ জনের বয়সের সমষ্টি/ ১০ 
আবার মনে করুন, তিন বন্ধুর গড়(Average) আয় ২০০০ টাকা।  
অতএব, তাদের মোট আয় = ২০০০X ৩ = ৬০০০ টাকা 

গড়ের(Average) অংকের মজা হল: আপনি প্রশ্ন পড়তে পড়তে অংক করবেন। প্রথম লাইনে যা আছে তা দিয়ে অংক করা শুরু করবেন। ২য় লাইনে কিছু দেওয়া থাকলে তা প্রয়োগ করবেন। দেখবেন, প্রশ্ন পড়া শেষ হওয়ার আগেই আপনার অংক শেষ। 
চলুন চেষ্টা করি:

পিতা মাতা ও পুত্রের বয়সের গড়(Average) ৩৭ বছর। আবার পিতা ও পুত্রের বয়সের গড় ৩৫ বছর।মাতার বয়স কত?

প্রথম লাইনে আছে, পিতা মাতা ও পুত্রের বয়সের গড়(Average) ৩৭ বছর
তাহলে, পিতা মাতা ও পুত্রের মোট বয়স = ৩৭X = ১১১ বছর 
২য় লাইনে আছে, পিতা ও পুত্রের বয়সের গড়(Average) ৩৫ বছর
তাহলে, পিতা ও পুত্রের মোট বয়স =(৩৫X ২) = ৭০ বছর 

তাহলে, মাতার বয়স = (১১১-৭০) = ৪১ বছর।  

M সংখ্যক সংখ্যার গড়(Average) A এবং N সংখ্যক সংখ্যার গড় B ,সবগুলো সংখ্যার গড় কত?
প্রথম লাইনে আছে,
M সংখ্যক সংখ্যার গড়(Average) A
তাহলে M সংখ্যক সংখ্যার সমষ্টি = M X A= MA
২য় লাইনে আছে,
N সংখ্যক সংখ্যার গড়(Average) B
তাহলে N সংখ্যক সংখ্যার সমষ্টি = N X B= NB

তাহলে গড়(Average) = মোট সমষ্টি / মোট সংখ্যা = (MA+NB)/(M+N)

দুইটি গড়(Average) দেওয়া থাকলে, প্রথমে তাদের সমষ্টি বের করে নিবেন।  তারপর আবার ভাগ করবেন।  

আরেকটি অংক দেখি:
একজন শ্রমিক প্রতিদিন প্রথম ৮ ঘন্টা কাজ করার জন্য ঘন্টায় ১০ টাকা করে এবং পরবর্তী সময়ের জন্য ঘন্টায় ১৫ টাকা করে মজুরি পায়। দৈনিক ১০ ঘন্টা করে কাজ করলে ঘন্টা প্রতি গড়(Average) মজুরি কত?

প্রথম ৮ ঘন্টা কাজ করার জন্য ঘন্টায় ১০ টাকা করে  মোট ৮০ টাকা পায় 
পরবর্তী সময়ের জন্য ঘন্টায় ১৫ টাকা করে মজুরি পায়।  
তাহলে ২ ঘন্টায় পায় = ৩০ টাকা 
মোট মজুরী পায় = ১১০ টাকা 
মোট কাজ করে ১০ ঘন্টা 
অতএব, গড়(Average) মজুরি = ১১ টাকা। 

Practice-1:

পিতা মাতা ও পুত্রের বয়সের গড়(Average) ৩৭ বছর। আবার পিতা ও পুত্রের বয়সের গড় ৩৫ বছর। মাতার বয়স কত?

Solution:

পিতা মাতা ও পুত্রের বয়সের গড়(Average) ৩৭ বছর

পিতা মাতা ও পুত্রের মোট বয়স=৩৭×৩=১১১

পিতা ও পুত্রের মোট বয়স=৩৫×২=৭০

মাতার বয়স=(১১১-৭০)=৪১ বছর

Practice-2:

১৫ জন ছাত্রের প্রাপ্ত নম্বরের গড়(Average) ১০ এবং ১০ জন ছাত্রের প্রাপ্ত নম্বরের গড় ১৫। সকল ছাত্রের প্রাপ্ত নম্বরের গড় কত?

Solution:

১৫ জনের সমষ্টি=১৫×১০=১৫০

১০ জনের সমষ্টি=১৫×১০=১৫০

অতএব গড়(Average) =    ১৫০+১৫০/২৫  =১২

Practice-3:

তিন বন্ধুর ওজনের গড় (Average)৩৩ কেজি।তিন জনের মধ্যে কোন বন্ধুর ওজনই ৩১ কেজির কম নয়। তিন বন্ধুর এক জনের সর্বোচ্চ কত হতে পারে?

Solution:

ওজনের সমষ্টি =৩৩×৩=৯৯

দুজনের নূন্যতম অজন হবে=(৩১×২)=৬২ কেজি

একজনের সর্বোচ্চ ওজন=৯৯-৬২=৩৭ কেজি।

Practice-4:

একজন দোকানদার ১২ দিনে ৫০৪ টাকা  আয় করে। তার প্রথম চারদিনের গড়(Average) আয় ৪০ টাকা হলে অবশিষ্ট দিনগুলির গড় আয় কত?

Solution:

৪ দিনের আয়=৪×৪০=১৬০ টাকা

১২ দিনে আয়=৫০৪ টাকা

৮ দিনের আয়=(৫০৪-১৬০)টাকা

গড়(Average) আয়=১৪৪/৮=৪৩ টাকা।

Practice-5: 

P এবং Q এর সমষ্টি ৭২। R এর মান ৪২। P,Q এবং R এর গড়(Average) কত?

Solution:

P,Q এবং R এর সমষ্টি = ৭২ + ৪২ = ১১৪

P,Q এবং R এর গড়(Average) = ১১৪/৩ = ৩৮

Practice-6: 

X নামক এক কোম্পানির ১০ জন কর্মচারীর বেতনের গড়(Average) ৩০০০০ টাকা। কোম্পানীর অন্য ৩০ জন কর্মচারীর বেতনের গড় ৪০০০০ টাকা। কোম্পানীর অবশিষ্ট ২০ কর্মচারীর বেতনের গড় ৬০০০০ টাকা। কোম্পানীর ৬০ জন কর্মচারির বেতনের গড় কত?

Solution:

১০ জন কর্মচারীর বেতন = (৩০০০০ X১০)= ৩০০০০ টাকা

৩০ জন কর্মচারীর বেতন = (৪০০০০x৩০)=১২০০০০ টাকা

২০ জন করমচারীর বেতন = (৬০০০০x২০)=১২০০০০ টাকা
তাহলে , (১০+৩০+২০) জন বা ৬০ জন এর বেতন = (৩০০০০০+১২০০০০০+১২০০০০০) টাকা = ১৮০০০০ টাকা

তাহলে , গড়(Average) বেতন = (১৮০০০০/৬০) টাকা = ৪৫০০০ টাকা