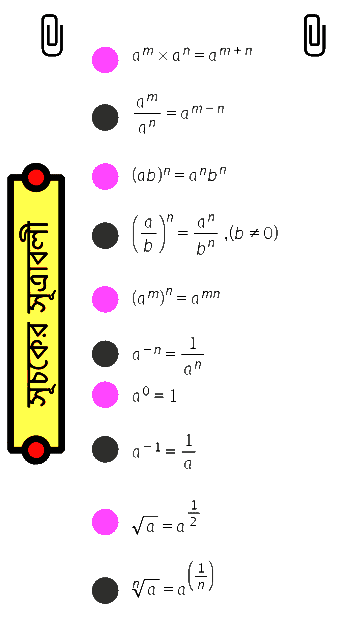সূচক ও লগারিদমের সূত্র ও প্রয়োগ

সূচক ও লগারিদম
(BCS প্রিলিমিনারিতে সূচক ও লগারিদম, সমান্তর ও গুণোত্তর অনুক্রম ও ধারা থেকে সর্বোচ্চ ০৩ নম্বর থাকবে এবং অন্যান্য প্রতিযোগিতামূলক পরীক্ষায়ও এ অধ্যায়গুলো থেকে প্রশ্ন থাকে)
সূচক ও লগারিদমের সূত্র সমূহ গণিতশাস্ত্রের ক্ষেত্রে গুরুত্বপূর্ণ। আপনি গনিতের ক্যালকুলাস থেকে শুরু করে জ্যামিতিক বিভিন্ন সমস্যা সমাধানের ক্ষেত্রে সূচক ও লগারিদমের ব্যবহার করতে দেখতে পারেন। সূচক ও লগারিদম সম্পর্কে আমাদেরকে উচ্চ বিদ্যালয় থেকে ধারণা দেওয়া শুরু করা হয় কেননা পরবর্তীতে বিভিন্ন গাণিতিক সমস্যা সমাধানের ক্ষেত্রে সূচক ও লগারিদমের বিভিন্ন সূত্রের ব্যবহার করতে হবে। আজকে আমরা সূচক ও লগারিদমের সূত্র সমূহ সম্পর্কে জানাব। সূত্রগুলো যাতে আমরা অনুশীলন করতে পারি এজন্য পিডিএফ ফাইলের লিঙ্ক দেয়া হয়েছে
লগারিদম কী ?
লগারিদম হচ্ছে পাওয়ারের বিপরীত তত্ত্ব। যেমন দেখুনঃ
23 =2 x 2 x 2 =8
লগারিদমে এটিকে প্রকাশ করা হয়,
log2 8 = 3. যেখানে 2 হল লগের বেইস, 8 হল লগের পাওয়ার।
23=8 —> log2 8 = 3; পাওয়ার ডান পাশে চলে আসবে।
20=1 —> log2 1 = 0
51=5 —> log5 5 = 1
শুধু ধনাত্মক সংখ্যারই লগারিদম আছে, শূন্য বা ঋণাত্মক সংখ্যার লগারিদম নেই।
লগারিদমের সূত্র সমূহ
লগারিদমের অনেকগুলো সূত্র রয়েছে। এরমধ্যে সব ক্ষেত্রে ব্যবহৃত হয় এমন কিছু সূত্র এখানে দেয়া হলো। এই সূত্রগুলো লগারিদমের বেসিক কিছু সূত্র:
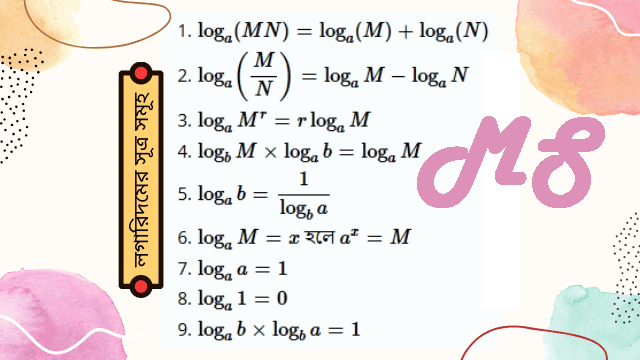
লগারিদম-সম্পর্কিত মৌলিক কিছু বিষয়:
(i) লগের সংজ্ঞানুসারে loga1 = 0 বা সাধারণভাবে log1=0 অর্থাৎ যেকোনো ভিত্তিতে লগের পাওয়ার 1 হলে তার মান শূন্য হয়।
(ii) লগের সংজ্ঞানুসারে logaa = 1 অর্থাৎ লগের ভিত্তি এবং লগের পাওয়ার একই হলে তার মান 1 হয়।
(iii) একই ভিত্তির সাপেক্ষে দুই বা ততোধিক সংখ্যার গুণফলের লগারিদম ওই একই ভিত্তির ওপর সংখ্যাগুলোর পৃথক পৃথক লগারিদমের সমষ্টির সমান,
অর্থাৎ, loga(M´N) = logaM+logaN এবং
(iv) একই ভিত্তির সাপেক্ষে দুটি সংখ্যার ভাগফলের লগারিদম, ওই একই ভিত্তির ওপর সংখ্যা দুটির পৃথক পৃথক লগারিদমের বিয়োগফলের সমান,
অর্থাৎ, loga(M÷N) বা loga M/N = logam – logaN
(v) সূচকযুক্ত সংখ্যার লগারিদম, ওই সূচক ও ওই সংখ্যার লগারিদমের গুণফলের সমান অর্থাৎ logaMr = rlogaM
(vi) যদি লগের বেইস উল্ল্যেখ না থাকে তবে ধরে নিতে হবে প্রদত্ত অংকে সব লগারিদমের বেইস সমান।
কিছু সমাধানঃ
log28=কত?
log28 = log223
এখন সূচকযুক্ত সংখ্যার লগারিদম, ওই সূচক ও ওই সংখ্যার লগারিদমের গুণফলের সমান
অর্থাৎ logaMr = rlogaM
তার মানে log223 = 3 log22
লগের সংজ্ঞানুসারে logaa = 1
অর্থাৎ লগের ভিত্তি এবং লগের পাওয়ার একই হলে তার মান 1 হয়।
অর্থাৎ 3 log22 = 3×1 = 3
log2(1/32) এর মান-
log 2(1/25) = log22-5= -5 log22 = -5×1 = -5
সূচক কী ?
সূচকের সংক্রান্ত পর্যালোচনা
সুতরাং আমরা বলতে পারি, যে সংখ্যার সাহায্যে কোনো নির্দিষ্ট বৎসর বা সময়ের সাথে অন্য কোন বৎসর বা সময়ে কোন দ্রব্যের মূল্য বা উৎপাদনের আপেক্ষিক পরিবর্তনের আনুপাতিক হার নির্দেশ করা হয় তাকে সূচক সংখ্যা বলে।
সূচকের সূত্র সমূহ